James (Jim) Frankenfield - Academic Library - Math Videos
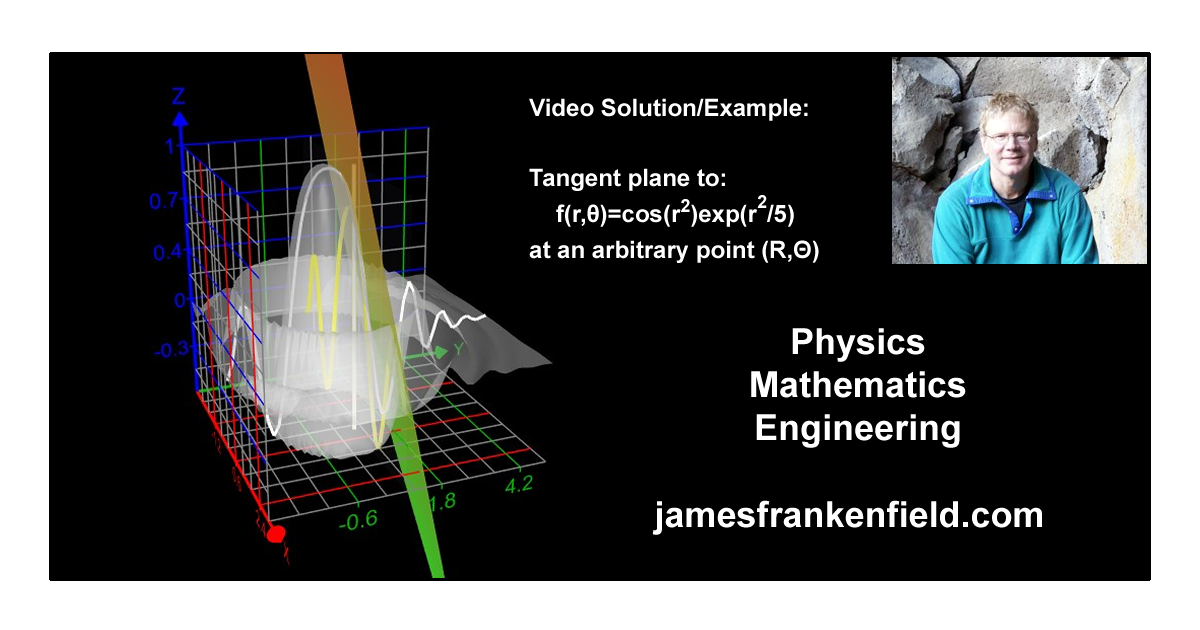
Problem Solution #14 - Math - The tangent plane to f(x,y) at point (a,b)
A text summary of the problem and solution are below, along with a link to the Desmos page used and the problem file for "Graphing Calculator 3D"
.
I have a few videos on YouTube which I produce and post as part of my tutoring and teaching work. If you find them helpful please like the video and the channel and it will encourage me to make more. You can also suggest or request a topic via my contact page. I will consider requests but at the moment cannot make too many videos too quickly.
Problem Solution #14 - Math - The tangent plane to f(x,y) at point (a,b)
A question about this problem was posed on a help group by a math major. She was confused about the cross product. The problem is to find the plane tangent to a surface f(x,y) at a given point (a,b). In this video I go through the entire problem (including the cross product part) and use "Graphing Calculator 3D" by Runiter.com to illustrate the process.
This is an advanced problem from multi-variable calculus. However, I think astute students not yet at that point may be able to follow along with what I do in the video with the exception of the paper/pen actual calculus work. The graphical explanations should be more intuitive, and the 3D graphs are a great tool. I was quite excited to find this Runiter.com free tool.
If you need math help, including at lower levels, then feel free to contact me for tutoring! I can help with math, physics and engineering at all levels on almost all topics.
As usual the Desmos page for this video is available and can be found here. And if you have the Graphing Calculator 3D then here is the file I use in the video. I make all supporting materials freely available for all of my videos.
Summary of finding the tangent plane to f(x,y)
This is also summarized in the video introduction on youtube. First, due to the symmetry of the problem, we can rewrite f(x,y) in cylindrical coordinates as f(r,θ). It does not depend on θ so we can first look at this in 2 dimensions on any vertical plane through the origin, which we do on Desmos.
First we need functions which trace a path along the surface in 2 perpendicular dimensions, in the photo above the yellow and white are in the x and y directions. But it's easier to work in the r and θ directions so we do that for the solution on paper. If we take the partial derivatives along these paths at the point of interest (a,b) we have two tangent vectors at the point. By definition these are in the tangent plane, of course. But to find that equation we take a cross product to get a vector normal to the plane we want. And from that, after going back to (x,y) from (r,θ), we get the plane equation.
Using Graphing Calculator 3D we can show this plane, and we can change (a,b) to see it wherever we want. In the video I hold x or y constant and increase the other (i.e. moving the point out in the radial direction) and we can see something analogous to what we had in our Desmos 2D version. I also keep r constant and vary θ and you can see the plane move around the surface at a fixed height (and r). You can get the grapher for free and my file is available below, so feel free to play with this yourself if you are interested.
The solution is worked out on paper in addition to being visualized and explained in the video, and you can also access the Desmos page which is used. And if you want to use my 3D file it is here.