James (Jim) Frankenfield - Academic Library - Physics Videos

Problem Solution #10 - Physics - Projectile Motion and Parabola Problem

A text summary of the problem and solution are below, along with a link to the Desmos page used.

I have a few videos on YouTube which I produce and post as part of my tutoring and teaching work. If you find them helpful please like the video and the channel and it will encourage me to make more. You can also suggest or request a topic via my contact page. I will consider requests but at the moment cannot make too many videos too quickly.

YouTube Channel

Problem Solution #10 - Physics - Projectile/Parabola Problem

This problem was probably posed by a math teacher as a parabola problem but it was cast in terms of a kinematics problem with a basketball being thrown upwards. Upon investigating the problem in some detail we find that the math solution implies an acceleration of gravity of 1.088 and not the 9.8 we assume for earths surface. Does your math teacher or tutor know enough about physics or other applications to write realistic application problems? Will your tutor notice anything wrong in a case like this? And if the discrepancy is pointed out to them will they be able to come up with an explanation or analysis? If not then feel free to contact me for tutoring! (I see more and more tutors asking where to find solutions manuals, apparently because they can't solve the books problems themselves. If the book solved this one way and they did it another way and disagreed then what would they do?)

As usual the Desmos page for this video is available and can be found here. I make all supporting materials freely available for all of my videos.

The Parabola/Projectile Desmos Page

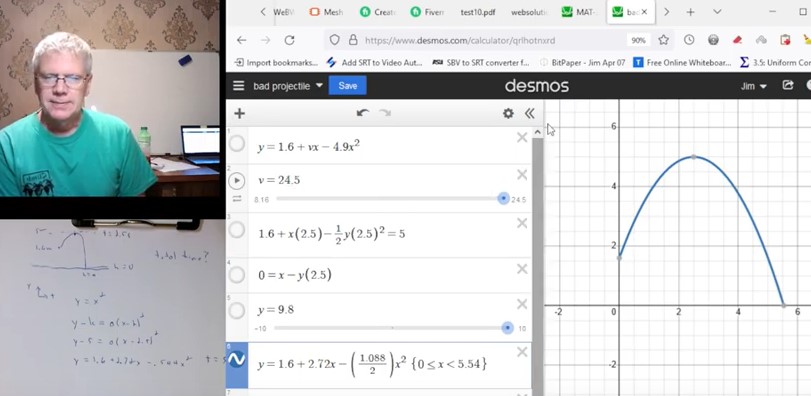
Summary of the Projectile Motion Problem and Solution

 

This problem states that a basketball is thrown upwards from an initial height of 1.6 meters, reaches a maximum height of 5 meters after 2.5 seconds, then falls down to the ground (height of zero). So we are given 3 parameters as fixed. We also know from basic physics that the velocity (instantaneous) is zero at the top (5m, 2.5s) where it changes from going up to going down. We also generally assume we are on the surface of the earth where the acceleration due to gravity is g or 9.8 m/s².

First we solve this strictly as a math problem. The graph of height (y) vs. time (t) is a parabola and we have two points: (0,1.6) and (2.5,5). We can find a parabola that fits these points and then solve the quadratic for t when y is zero. This all seems simple enough. But we have not considered the physics at all here so perhaps we should check that out.

We know that velocity v is zero at the top when t is 2.5 seconds and we are assuming acceleration is g or 9.8, so we can use our kinematics velocity equation to find initial velocity v_o. We can use v_o in the height equation and find the time when y is zero. Note that we only assumed the time to the top is 2.5 and that v there is zero, we did not consider the height of 5 at all in our calculations.

We can also use the height equation applied from the top to the ground, as if we are dropping the ball. Initial velocity v_o is zero in this case and initial height is 5 while the final is zero. And we use g or 9.8 again for acceleration. We can add this falling time to the 2.5s it took to get to the top for a total time and we find it is quite different from our previous solutions (which did not agree either but were closer). In this case we did not consider the velocity at all, at any point. Nor did we use the time of 2.5s in our calculations, we just accepted that and added to it.

So we can see that our results are not consistent. What's really going on here?

Well, we have many constraints and in each approach we use some and not others. The math solution ignored all physics. The first solution ignored height. And if we go back and calculate the height at 2.5 seconds it is about 32m, not even close to 5! In the second physics solution we used the height of 5 but ignored velocity and the 2.5s, and we find that the initial velocity v_o needs to be 8.16 and the time to the top is not 2.5 seconds but rather 0.84 seconds. These constraints are inconsistent and our result depends on which ones we rely on and which ones we leave out.

As a final effort let's consider what is stated and take that as fixed and then vary what was not explicitly stated. So the 1.6m, 2.5s, and 5m will be fixed. (And we still assume that v is zero at the top, which is required.) So the only two things we can vary in our kinematics equations are initial velocity v_o and the acceleration. It's highly unusual to consider an acceleration of other than g in a problem like this but what else can we do here? (Usually if there is some other gravity constant it would be given, perhaps for something on the moon or a planet. But this is a basketball problem!) Our kinematics equations give us two linear relationships between initial velocity v_o and acceleration (which we label g, even though g is technically used specifically for 9.8 on earth).

When we solve the simultaneous linear equations we find values for v_o and g. And the gravity acceleration turns out to be 1.088! I believe this would apply somewhere beyond most or all satellites but closer to earth than the moon is. Obviously the problem was not properly written/specified. When we put in our numbers for v_o and g we get the original math solution. Which makes sense since we need to go through the two specified points if we take those as fixed and not changeable. So we need the math solution in the end but we find that it defies the laws of physics and is not realistic. And treating this as the kinematics problem it is from the start would lead us down a confusing path. (Whereas treating it as a math problem and calling it good would probably give the intended answer and we could very well remain ignorant of the physics issues.)

The process is worked out on paper in the video, and you can also access the Desmos page which is used.